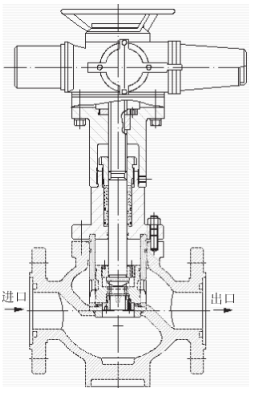
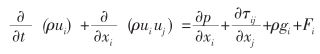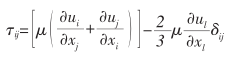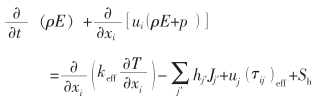图1 调节阀结构
1 数学模型的建立
在流体运动中遵循三个最基本的守恒方程,即质量守恒定律、动量守恒定律和能量守恒定律。通过网格划分就可以把流体模型划分成多个控制体,对于每一个控制体运用流体运动的三个基本方程进行模拟计算和分析。
连续性方程的微分形式为:
连续性方程又称质量守恒方程,该方程可用于可压流动和不可压流动。
动量守恒方程为:
式中 p——静压;
τij——应力张量,其表达式为
gi——i方向上的重力体积力;
Fi——i方向上的外部体积力。
能量守恒方程为:
式中 keff——有效热导系数;
Jj′——组分j′的扩散通量;
Sh——化学反应热和其他体积热源。
其中,keff=kt+k。方程右边前三项为导热项、组分扩散项和黏性耗散项。
对于理想气体,
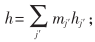
对于不可压缩气体,

2 调节阀流道结构建模与网格划分
2.1 调节阀流道的结构建模
本文采用某型号调节阀,运用三维建模软件建立调节阀的实体模型,通过布尔运算抽取调节阀及加长管道部分。为了更好更准确地模拟阀体内部流动情况,对阀出口管段进行加长,加长管道的长度大约为250mm(约为管道直径的5倍)。图2所示为调节阀开度为10%时流道的剖面实体模型。
图2 调节阀10%开度时流道剖面
2.2 计算网格的划分
将调节阀流道的三维实体模型导入ANSYSWorkbench(网格划分)软件中进行数值模拟计算的前处理。为了节省计算时间,建立流道模型的一半作为计算模型。为了提高计算精度和考虑数值计算对计算机的要求,在划分网格时采用非结构化的四面体网格。划分后的网格数大约为5万左右。设置边界条件为压力入口和压力出口,流道模型剖面设置为对称面边界。调节阀开度为10%的流道网格划分如图3所示。
图3 调节阀流道网格
3 数值计算与结果分析
3.1 边界条件设置
将处理后的网格文件导入Fluent分析模块,并进行边界条件和流体属性设置,选择合适的求解方程及模型。设置流体属性为ideal-gas,流体属性参数保持默认值。设置入口和出口压力,使得压差分别为0.4MPa、0.55MPa、0.66MPa、0.7MPa,并分别进行数值模拟计算。湍流模型选用Spalart-Allmaras湍流模型(S-A方程湍流模型)。S-A方程湍流模型常用于大梯度和近壁气体流动的数值模拟。不同开度和不同压差下的数值模拟计算结果如表1所示。
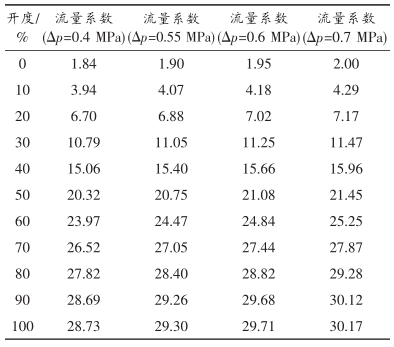
表1 不同开度和不同压差下数值模拟的流量系数值
3.2 流量系数的结果分析
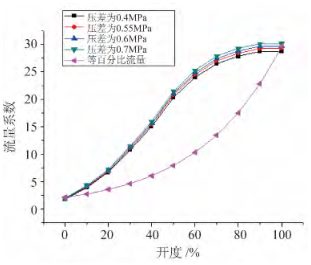
从表1可以看出,在同一压差条件下,调节阀的流量系数随开度的增加而增大,开度越大调节阀流量系数也越大,当调节阀为全开状态时流量系数最大。在同一开度条件下,调节阀的流量系数随着压差的增大而增大,进出口压差越大调节阀的流量系数也越大。从图4可以看出,不同压差下调节阀流量特性曲线吻合较好,流量特性基本一致。在开度较小时,由于调节阀前后的压差作用,调节阀的流量会呈现快速增长的趋势,从而使得流量系数在小开度时增长较快。在开度较大时,调节阀流量基本趋于稳定,流量系数的增长较慢缓。在开度小于60%时,调节阀的流量特性与等百分比流量特性趋势基本一致;在开度较大时,与等百分比流量特性相比,调节阀流量特性有下降趋势。
图4 不同压差下的流量系数与等百分比流量特性曲线对比
4 数值模拟结果分析
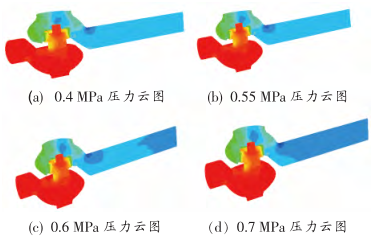
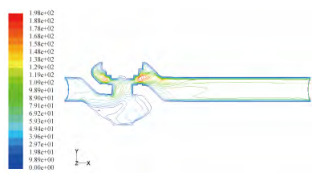
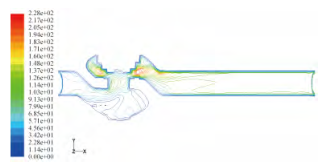
对开度为50%时调节阀在不同压差下的流场进行分析。选取不同压差下的压力云图和压差为0.4MPa、0.6MPa的速度等值线图进行分析。从图5~图7可以看出,压力和速度变化最大的地方出现在阀芯启闭的部位。在阀门出口的拐角处也出现了明显的压力和速度值的变化,该处压力和速度值的变化是由于产生涡漩造成的。在阀门的进出口位置和阀腔内流体流动比较均匀,压力和速度值保持恒定。流体的最大流速还与阀的前后压差成正比关系,随调节阀前后压差的增大而增大,并且调节阀的最大速度出现在阀芯启闭部位。由能量守恒可知,在阀门压力大的地方流体的流速相对较小,流体流速最大的部位流体压力值最小。
图5 不同压差下的压力云图
图6 0.4MPa压差时的速度等值线图