多重阀门关闭降低高压管道水击压力的机理和实验研究

方面团员

摘 要 高压管道中阀门的关闭会产生水击压力，水击压力过大会破坏管道系统，造成严重的安全事故。提出一种多重阀门关闭降低水击的新方法。为了得到管道内水击压力，采用CFD软件仿真进行计算。多重阀门关闭方法相较于一般的单个阀门关闭，有效地降低了管道中产生的水击压力;并通过试验验证了多重阀关闭方法的有效性。在此基础上完成了双阀门关闭

模型的各参数影响水击压力数值的模拟仿真计算，得到上游阀门开度!阀门关闭速度!两阀门间距对水击压力的影响规律。通过对比三阀门关闭模型的水击压力模拟 仿真计算，得到双阀门是最优选择的结论。研究结果提出了一种降低高压管道中的水击压力的新方法，对高压管道的安全输送有重要意义。

关键词 水击 模拟仿真 高压管道 阀门

在高压管道中，关闭阀门时，会使液体的流速突变，引起管道中流体压力迅速增加或下降，即水击现象。发生水击现象，流体内压强急剧升高，达到一般管道正常工 作下压强的几十甚至上百倍。同时，水击也会产生很大的负压%这样大幅度的压强变化会对管道系统造成严重的安全事故。现有水击预防措施有:在条件允许下，加 大管径，降低流量，可以降低产生的水击压力;适当延长阀门关闭时间;在容易产生冲击的管道部位采用橡胶软管或者蓄能器吸收水击压力，或者安装安全阀限制压力升高。

但是，往往因为实际条件不允许，因此为降低水击作用。本文提出双阀门控制关闭的方法。在原有单阀门基础上新安装一个阀门，利用两个阀门配合关闭的方式降低水击压力双阀门关闭方法对现有管道改造较少，易安装，适用于大部分管道。

水击的计算方法常用的有特征线法、有限、元法、有限差分法等。特征线法是最为成熟的算法，计算效率高，能得到较为准确的结果，但不能很好的解决多特征差值 问题和非积分项的误差问题。随着计算机技术的发展，CFD软件可用于对水击压力模拟仿真计算，华晔、廖伟丽通过CFD计算水击压力与实测值相差仅为 2.7%。

本文利用CFD仿真计算，对管道阀门关闭进行模拟，在本文所用参数下，双阀门关闭方法相对于普通单个阀门关闭，水击压力的峰值降低20%以上。

本文还分别对阀门的关闭速度，上游阀门关闭的程度，各阀门之间的距离对水击压力的数值影响进行仿真计算，并得到一系列规律。通过与三阀门关闭的结果进行对比，双阀门模型是最优的选择研究结果对降低高压管道内的水击压力有重要意义。

1 数学模型

管道中存在高速高压流体并迅速关闭阀门是湍流瞬态问题，必须考虑流体的压缩性。因此采用雷诺平均N-S方程和K-ε湍流模型。

流体的连续方程和动量方程为: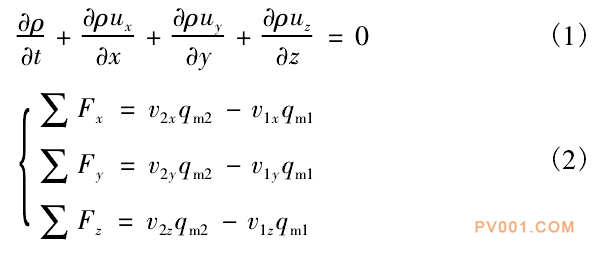

2 有限元模型建立

2.1 计算模型

选取25 m长的管道，阀门选择球阀。 管道直径为0.12 m，阀门距出口0.5 m，阀门半径为0.09 m，阀门关闭速度为匀速。计算可知，阀门旋转84°时达到完全关闭状态。由于模型形状为圆柱(图1)，在此仿真中可简化为二维模型，相对于三维模型，二维 模型能大大减少计算时间，并且可以将网格更加细化，得到结果更加准确，对模型进行网格划分，阀门处网格如图2所示。

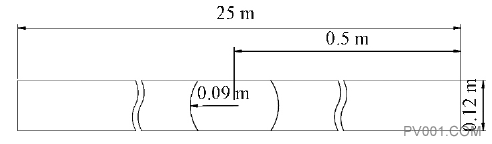
图1流道模型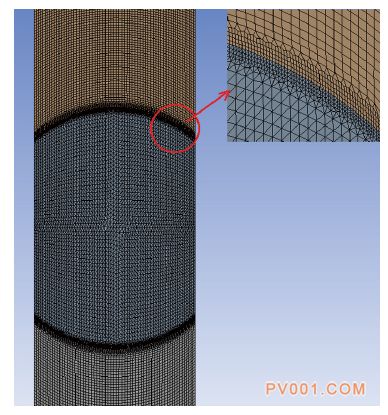

图2阀门流道网格划分

2.2 边界条件

选择双精度求解去进行求解;选择k-ε标准湍流模型;材料选择可压缩液态水;在计算域中将阀门流道选择滑移网格，根据所设置的运动形式用UDF编译并控 制;进口为压力进口，设置为0.4 MPa，出口为压力出口，设置为0 MPa ;阀和管道接触部分有数据交换，将接触部分，即两对弧线，设置为inter-face类型，并创建对应的mesh interface。设置监视器，记录静压力变化，数据类型为area-veighted aver-age;根据所定义的阀的角速度选择时间步长和步数，最后开始计算。

3 单、双阀模型对比与验证

3.1 单阀模型计算结果

在管道中只有一个阀门时，让流体流通一段时间，运动稳定后关闭阀门，观察管道内距阀门10 m处的水击压力，如图3所示。水击压力曲线与郭兰兰等得到的具有相似规律，初步验证了此CFD软件仿真计算的正确性。

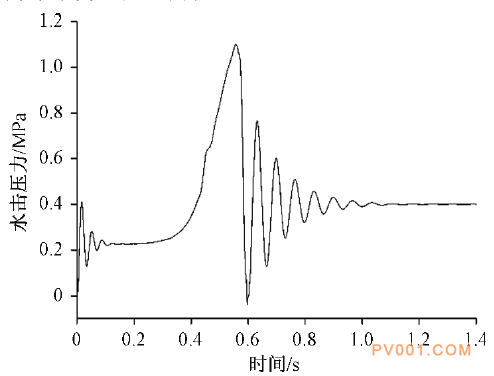
图3单个阀门关闭时水击压力

设置阀门关闭速度为πrad / s，阀门从0.1 s处开始关闭，0.567 s左右完全关闭。关闭阀门过程中，水击压力不断上升直到达到峰值1.1 MPa。阀门完全关闭后开始衰减波动，最后稳定在0.4 MPa左右。

3.2 双阀模型计算结果

在单阀管道基础上在上游添加一个阀门，两阀门之间相距0.5 m。流体流通一段时间稳定后，同时关闭两阀门。同样地，观察距下游阀门10 m处的水击压力。

阀门关闭速度与单阀模型相同，两阀门同时在0.1 s处开始关闭，关闭至0.567 s时刻停止，即完全关闭。双阀门关闭过程中，水击压力峰值0.857 MPa，水击压力衰减后稳定在0.4 MPa。

较图3和图5，双阀模型下管道内的水击压力峰值小于单阀模型，说明双阀门关闭能够减少水击压力。相比于单阀关闭，水击压力峰值降低22 %。

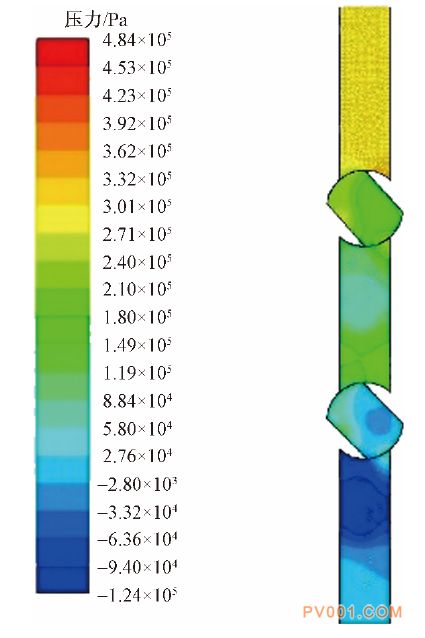
图4仿真静压云图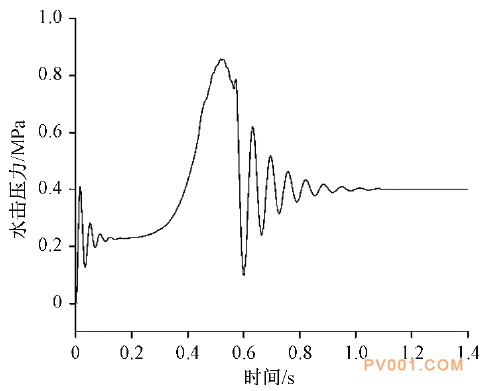

图5双阀关闭时水击压力

3.3 试验验证

试验设备包括试验台架、离心泵、流量传感器(2个)、压力传感器(2)、数据采集卡、计算机、PVC管、电磁阀(2个)、节流阀(1个)、止回阀(1个)，清水。流量为0.6 L/s。试验流程如图6所示。现场试验布置见图7。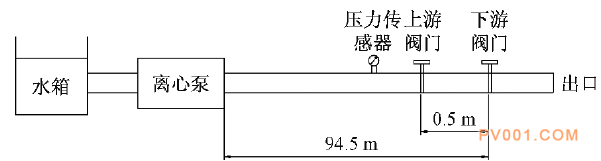

图6 试验流程简图

对单阀关闭模型进行试验，只关闭下游阀门，产生的水击压力曲线图见图8。

对双阀关闭模型进行试验，两阀门同时关闭，产生的水击压力曲线图见图9。

图7现场试验布置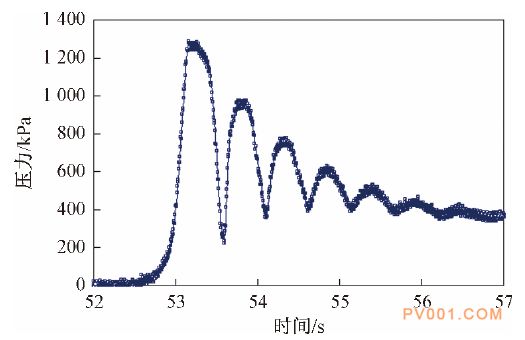

图8单阀关闭模型的水击压力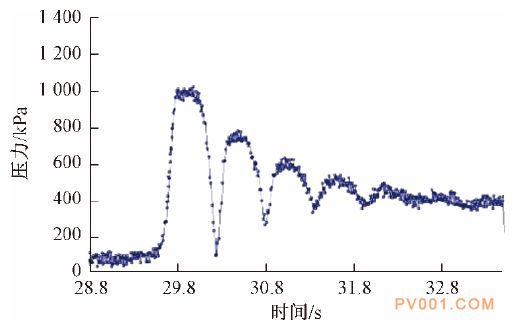

图9双阀关闭模型的水击压力

通过试验测得单阀关闭模型所产生的水击压力峰值约为1.3 MPa，双阀关闭模型所产生的水击压力峰值约为1 MPa，两者衰减后都稳定在0.4 MPa。

双阀关闭模型相对于单阀关闭模型，水击压力峰值降低23.1 %。由于衰减时间与管道长度有关，且仿真中管道为刚性，所以试验衰减时间大于仿真计算，水击压力变化最大幅度小于仿真值。对于双阀降低水击压力峰值，仿真 计算与试验具有较好的一致性，均证明双阀关闭模型能够有效的减少水击压力20%以上。

4 双阀各参数影响规律

4.1 上游阀门开度对水击压力影响规律

利用上述双阀模型，为研究上游阀门最终开度对水击压力的影响，其余参数不变，只改变上游阀门最终关闭状态开度分别为1,0.5,0。经过CFD仿真计算后，得到水击压力如图10所示。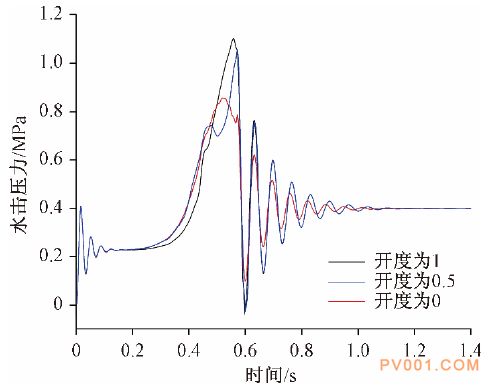

图10 上游阀门不同开度下的水击压力

在双阀关闭模型中，在单一变量的原则下，上游阀门最终开度越小，水击压力峰值越小，当上游阀门与下游阀门同时关闭，即最终开度为0时，水击压力峰值达到最小。

4.2 双阀门关闭速度对水击压力影响规律

在双阀门关闭过程中，上述实验关闭速度为πrad。为研究阀门关闭速度对水击压力峰值的影响，在单一变量原则下，将阀门速度分别设置为πrad , 0.8 π rad , 0.5π rad。经过CFD仿真计算后，得到水击压力曲线如图11所示。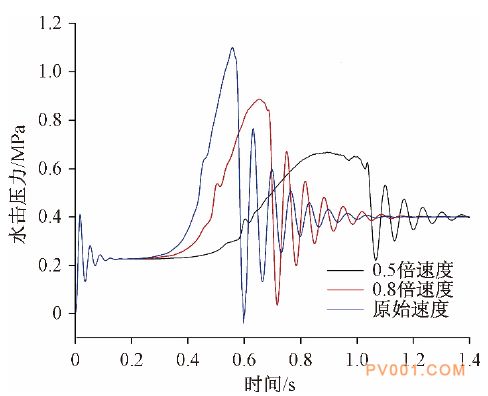

图11 阀门不同关闭速度下的水击压力

当阀门关闭速度越快时，管道中产生的水击压力产生的速度越快，其峰值越大，产生的负压越大，衰减速度也越快。最终平稳后，压力都趋近于0.4 MPa。试验中由于关阀速度与仿真不同，导致峰值数值上不同。

4.3 上下游阀门间距对水击压力影响规律

上述实验上下游阀门间距为0.5 m，在其他参数相同情况下，将阀门间距分别设置为:0.75 m,1 m,1.25 m。将上下游阀门同时关闭，得到水击压力曲线如图12所示。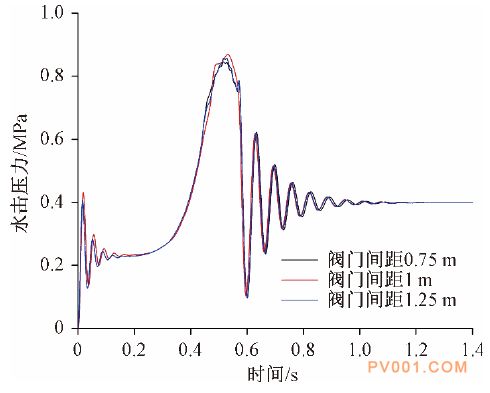

图12 不同阀门间距下的水击压力

图12中水击压力曲线几乎重合，阀门间距分别为0.75 m,1 m,1.25 m时，在同一位置测得的水击压力几乎相同。两阀门间距的大小对水击压力的数值几乎没有影响。

4.4 阀门个数对水击压力影响规律

为分析阀门个数影响，建立三阀门模型，在双阀门基础上再增加一个阀门，三个阀门两两之间间距0.5 m。利用CFD软件仿真三阀门同时完全关闭时，观察管道内水击压力的变化(图13)。其余参数与单、双阀模型相同。

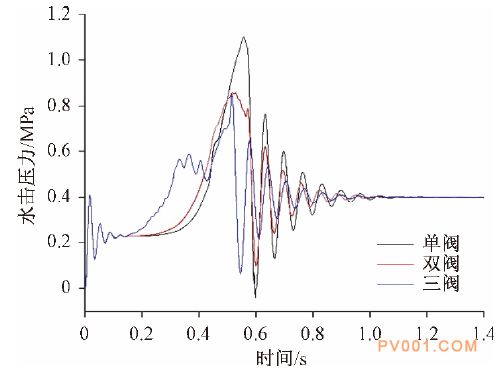
图13 各模型的水击压力

经CFD模拟计算，得到三阀门关闭模型管道中水击压力曲线，三阀模型水击压力产生速度最快，其次双阀门模型，最后是单阀门模型。三个模型衰减至稳定在 0.4 MPa用时相同。三阀门模型水击压力峰值为0.851 MPa，相对于单阀关闭模型，水击压力峰值降低22.6 %，相对于双阀关闭模型，水击压力峰值降低0.7 %。

5 结论

(1)利用CFD软件仿真计算分析双阀门关闭的方式对管道内水击压力变化的影响，发现双阀门关闭方式能有效降低水击压力，并通过清水试验验证了其正确性。

(2)对于双阀关闭模型:上游阀门最终开度越小，管内产生的水击压力越小;阀门关闭速度越快，管内水击压力产生越快，峰值越大，负压越大，衰减越快;阀门之间距离对管内水击压力几乎没有影响。

(3)建立三阀门关闭模型，在本文设置参数下，其管道内水击压力与单阀门关闭比较，水击压力峰值降低22.6 %;而与双阀门关闭比较，水击压力峰值仅降低0.7 %。从安装、改装难度和成本综合来看，双阀关闭模型是最优的。